COVID-19
This example illustrates just how fast exponential growth is. It was proposed on twitter by Charles Arthur (@charlesarthur) who attributes the idea to Simon Moores. The stadium version is a variant of the better known ‘grains of wheat (or rice) on a chessboard‘ problem. The stadium example is better, I think, because the time element gives it a sense of urgency, and that’s what we need right now.

Here’s Wembley Stadium. The watering system develops a fault: in minute 1 one drop of water is released; minute 2, two drops, minute 3 four drops, and so on. Every minute the number of drops doubles. How long will it take to fill Wembley stadium?
The answer is that after 44 minutes, before half-time, the stadium would overflow.
Here’s why.
The sequence is 1, 2, 4, 8, 16, . . . so the nth term in the sequence is 2n – 1. For example, the 4th term is 23 = 8.
Next we need to know how many drops are needed to fill the stadium. Suppose a drop of water has a volume of 0.07 ml. This is 0.00000007, or 7 x 10-8, cubic metres. Wembley Stadium has a volume of 1.1 million cubic metres. So the stadium holds 15,714,285,714,285 drops. Or about 15.7×1012 drops. How many minutes does it take to get to this volume of water?
After n minutes, the total volume of water will be the sum of all the drips up to that point. This turns out to be 2n-1. If this baffles you, check this video (in our case a =1 and r = 2).
We want to solve for n, the number of steps (minutes), 2n = 1 + 15.7×1012. The easiest way to do this is to take the logarithm of both sides.
n log(2) = log(1 + 15.7×1012).
So
n = log(1 + 15.7×1012) / log(2) = 44.8 minutes
At the 43rd minute the stadium would be more than half full: (243 – 1) = 8.80 x 1012, i.e. 56% of capacity.
By the 44th minute the stadium would have overflowed: (244 – 1) = 17.6 x 1012, i.e. 112% of capacity.
Notice that (after the first few minutes) in the nth minute the volume released is equal to the total volume that’s already in, so at the 44th minute an extra 8.80 x 1012 drops are dumped in. And at the 45th minute more than another stadium-full would appear.
The speed of the rise is truly terrifying.
Relationship of this to COVID-19
The rise in the number of cases, and of deaths, rises at first in a way similar to the rise in water level in Wembley stadium. The difference is that the time taken for the number to double is not one minute, but 2 – 3 days.
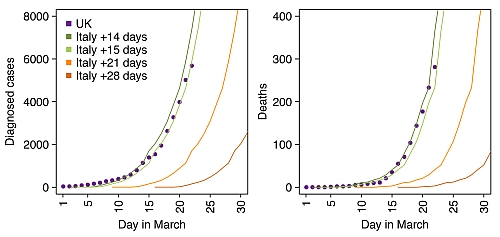
As of today, Monday 23rd March, both the number of diagnosed cases, and the number of deaths, in the UK are still rising exponentially. The situation in the UK now is almost exactly what it was in Italy 15 days ago. This from Inigo Martincorena (@imartincorena), shows it beautifully.


Boris Johnson’s weak and woolly approach will probably cost many thousands of lives and millions of pounds.
Up to now I’ve resisted the temptation to suggest that Whitty and Vallance might have been influenced by Dominic Cummings. After this revelation, in yesterday’s Sunday times, it’s getting progressively harder to believe that.

We have been self-isolated since March 12th, well before Johnson advised us it. It was obvious common sense.
Please stay at home and see nobody if you possible can.. This cartoon, by Toby Morris of thespinoff.co.nz, shows why.
Some good reading
The report from Imperial College, 16 March 2020, that seems to have influenced the government:
Tomas Pueyo. His piece on “Coronavirus: Why You Must Act Now“, dated March 10th, had 40 million views in a week
Tomas Pueyo. March 19th; What the Next 18 Months Can Look Like, if Leaders Buy Us Time.
“Some countries, like France, Spain or Philippines, have since ordered heavy lockdowns. Others, like the US, UK, or Switzerland, have dragged their feet, hesitantly venturing into social distancing measures.”
David Spiegelhalter. March 21st.
“So, roughly speaking, we might say that getting COVID-19 is like packing a year’s worth of risk into a week or two. Which is why it’s important to spread out the infections to avoid the NHS being overwhelmed.”
Washington Post. Some excellent animations March 14th
Up to date statistics. Worldometer is good (allows semi-log plots too).

