How big is the risk from eating red meat now? An update.

A new study of the effects of eating red meat and processed meat got a lot of publicity. When I wrote about this in 2009, I concluded that the evidence for harm was pretty shaky. Is there reason to change my mind?

The BBC’s first report on 12 March was uncritical (though at least it did link to the original paper -big improvement). On 16th March, Ruth Alexander did a lot better, after asking renowned risk expert, David Spiegelhalter. You can hear him talk about it on Tim Harford’s excellent More or Less programme. [Listen to the podcast].

David Spiegelhalter has already written an excellent article about the new work. Here’s my perspective. We’ll see how you can do the calculations yourself.

The new paper was published on Archives of Internal Medicine [get reprint: pdf]. It looked at the association between red meat intake and mortality in two very large cohort studies, the Health Professionals Follow-up Study and the Nurses’ Health Study.

How big are the risks from red meat?

First, it cannot be said too often that studies such as these observe a cohort of people and see what happens to those people who have chosen to eat red meat. If it were the high calorie intake rather than eating meat that causes the risk, then stopping eating meat won’t help you in the slightest. The evidence for causality is reconsidered below.

The new study reported a relative risk of death from any cause were 1.13 for one 85 g serving of red meat per day, and 1.20 for processed meat. For death from cardiovascular disease the risks were a slightly higher, 1.18 for read meat and 1.21 for processed meat, For dying from cancer the relative risks were a bit lower, 1.10 for red meat and 1.16 for processed meat.

A relative risk of 1.13 means that if you eat 85 g of red meat every a day, roughly a hamburger for lunch, your risk of dying in some specified period, e.g. during the next year, is 13 percent higher than that for a similar person who doesn’t eat the hamburgers.

Let’s suppose, for the sake of argument, that the relationship is entirely causal. This is the worst case (or perhaps the best case, because there would be something you could do). How big are your risks? Here are several ways of looking at the risk of eating a hamburger every day (thanks to David Speigelhalter for most of these). Later we’ll see how you can calculate results like these for yourself.

• If you eat a hamburger every day, your risk of dying, e.g in the coming year, is 13 percent higher than for a similar person who doesn’t eat hamburgers.
• In the UK there were around 50 cases of colorectal cancer per 100,000 population in 2008, so a 10% increase, even if it were real, and genuinely causative. would result in 55 rather than 50 cases per 100,000 people, annually.
• But if we look at the whole population there were 22,000 cases of colorectal cancer in the UK in 2009. A 10% increase would mean, if the association were causal, about 2200 extra cases per year as a result of eating hamburgers (but no extra cases if the association were not causal).
• Eating a hamburger a day shortens your life expectancy from 80 years to 79 years (sounds rather small)
• Eating a hamburger a day shortens your life by about half an hour a day, if you start at age 40 (sounds quite serious)
• The effect on life expectancy is similar to that of smoking 2 cigarettes a day or of being 5 Kg overweight (sounds less serious).
• The chance that the hamburger eater will die before the similar non-hamburger eater is 53 percent (compared with 50 percent for two similar people) (sounds quite trivial).

Clearly it isn’t easy to appreciate the size of the risk. Some ways of expressing the same thing sound much more serious than others. Only the first was given in the paper, and in the newspaper reports.

The results. Is there any improvement in the evidence for causality?

The risks reported in the new study are a bit lower than in the WCRF report (2007) which estimated a relative risk of dying from colorectal cancer as 1.21 (95% Confidence interval 1.04–1.42) with 50 g of red or processed meat per day, whereas in the new study the relative risk for cancer was only 1.10 (1.06-1.14) for a larger ‘dose’, 85 g of red meat, or 1.16 (1.09-1.23) for processed meat.

A 2010 update on the 2007 WCRF report also reported a similar lower relative risk for colorectal cancer of 1.16 for 100 g/day of red or processed meat This reduction in size of the effect as samples get bigger is exactly what’s expected for spurious correlations, as described by Ioannidis and others.

One reason that I was so sceptical about causality in the earlier reports was that there was very little evidence of a relationship between the amount of meat eaten (the dose) and the risk of dying (the response), though the reports suggested otherwise. The new study does seem to show a shallow relationship between dose and response, the response being the relative risk (or hazard ratio) for dying (from any cause).

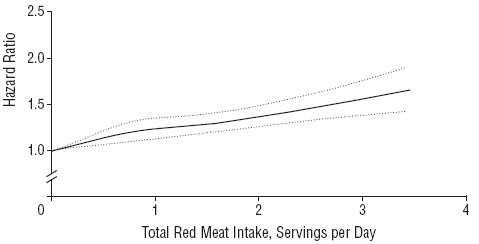
The Figure shows the relationship in the Nurses’ Health Study (it was similar for the other study). The dotted lines are 95% confidence limits (see here), and the lower limit seems to rule out a horizontal line, so the evidence for a relationship between dose and response is better than before, But that doesn’t mean that there is necessarily a causal relationship.

There are two important problems to consider. The legend to the figure says (omittng some details) that

"The results were adjusted for age; body mass index; alcohol consumption, physical activity level, smoking status ; race (white or nonwhite); menopausal status and hormone use in women, family history of diabetes mellitus, myocardial infarction, or cancer; history of diabetes mellitus, hypertension, or hypercholesterolemia; and intakes of total energy, whole grains, fruits, and vegetables." 

So the data in the graph aren’t raw observations but they’ve been through a mathematical mill. The corrections are absolutely essential, For example, Table 1 in the paper shows that the 20% of people who eat the most red meat had almost twice the total calorie intake of those who eat the least red meat. So without a correction there would be no way to tell whether it was high calorie intake or eating red meat that was causing an increased risk of death. Likewise, those who eat more red meat also smoke more, drink more alcohol, are heavier (higher body mass index) and take less exercise.

Clearly everything depends on the accuracy of the corrections for total calorie intake etc. It was done by a method called the Cox proportional hazard multiple linear regression. Like any other method that makes assumptions, and there is no easy way to check on how accurate the corrections are. But it is known "that studies on colon cancer that adjusted for larger number of covarariates reported weaker risk ratios than studies which adjusted for a smaller number". The main problem is that there may be some other factor that has not been included in the corrections. Spiegelhalter points out

"Maybe there’s some other factor that both encourages Mike to eat more meat, and leads to a shorter life.

It is quite plausible that income could be such a factor – lower income in the US is both associated with eating red meat and reduced life-expectancy, even allowing for measurable risk factors."

How to do the calculations of risk.

Now we come to the nerdy bit. Calculations of risk of the sort listed above can be done for any relative risk, and here’s how.

The effect on life expectancy is the hardest thing to calculate. To do that you need the actuaries’ life table. You can download the tables from the Office of National Statistics. The calculations were based on the “England and Wales, Interim Life Tables, 1980-82 to 2008-10“. Click on the worksheet for 2008 – 10 (tabs at the bottom). There are two tables there, one for males, one for females. I copied the data for males into a new spreadsheet, which, unlike that from ONS, is live [download live spreadsheet]. There is an explanation of what each column means at the bottom of the worksheet, with a description of the calculation method. In the spreadsheet, the data pasted from the full table are on the left.

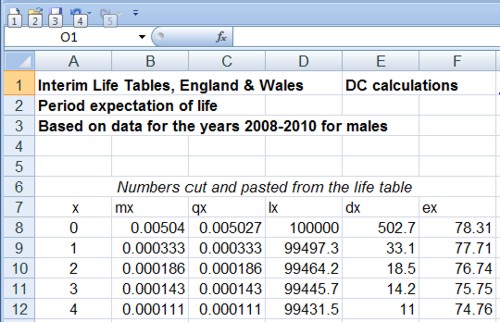
and lower down we see life expectancy, $ e_x $, from age 40 is 39.8 years

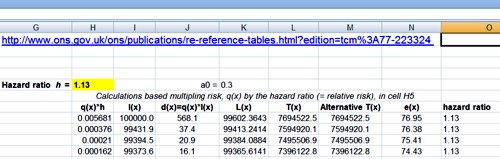
On the right is an extended life table which is live. You enter into cell H5 any relative risk (hazard ratio), and the table recalculates itself.

Lower down, we see that life expectancy from age 40 with risk ratio 1.13 is 38.6 years.

If you enter 1.00 on cell H5 (highlighted), the table on the right is the same as that on the left (there are some trivial differences because of the way that ONS does the calculations). The life expectancy of a 40 year old man is 39.8 years, so the average age of death is 79.8 years. If you enter 1.13 in cell H5, the relative risk of dying (from any cause) for a hamburger per day, the table is recalculated and the life expectancy for a 40 year old man falls to 38.6, so the mean age of death is 78.6 years (these numbers are rounded to 80 and 79 in the summary at the top of this page).

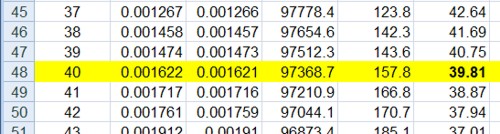
The Excel sheet copies the relative risk that you enter in cell H5 into column O and uses the value in column O to multiply the risk of death in the next year, $ q_x $. So, for example, with a hazard ratio of 1.13, the risk of dying between 40 and 41 is increased from $ q_{40} = 0.00162 $ to $ q_{40} = 0.00162 \times 1.13 = 0.00183 $, and similarly for each year. If you want the relative risk to vary from year to year, you can enter whatever values you want in column O.

Loss of one year from your life expectancy when you are 40 implies loss of about half an hour per day of remaining life: (365 x 24 x 60)/(40 x 365) = 36 minutes per day. This is close to one microlife per day. A microlife is defined as 30 minutes of life expectancy. A man of 22 in the UK has 1,000,000 half-hours (57 years) ahead of him, the same as a 26 year-old woman. David Spiegelhalter explains that loss of one microlife per day is about the same risk as smoking two cigarettes per day. This is put into perspective when you realise that a single chest X-ray will cost you two microlives and a whole-body CT scan (which involves much larger exposure to X-rays) would cost you 180 microlives.

The last way of expressing the risk is perhaps the most surprising. The chance that someone who has a hamburger for lunch every day will die before a similar non-hamburger eater is 53 percent (compared with 50 percent for two similar people). This calculation depends on a beautifully simple mathematical result.

The result can be stated very simply, though its derivation (given by Spiegelhalter here, at the end) needs some maths. The probability that the hamburger eater will life longer than the non-hamburger eater is

\[ \frac{1}{h+1}. \]

When there is no risk, $ h = 1$, this is 0.5, a 50:50 chance of one person dying before the other. When the relative risk (hazard ratio) is $ h = 1.13 $ it is
\[ \frac{1}{1.13+1} = 0.47, \]
so there is a 100 – 47 = 53% chance that hamburger eater dies first.

Another way to put the same result is to say that when a hazard ratio, $ h $, is kept up throughout their lives, the odds that hamburger eater dies before the non-hamburger eater is precisely $ h $. The odds of an event happening are defined as the ratio between the probability of it happening, $ p $, to the probability of it not happening, $ (1-p) $, i.e.
\[ h = \frac {p} {(1-p)}. \]
Rearranging this gives
\[ p = \frac {h} {(1+h)}. \]
When the risk ratio is $ h=1.13 $ this gives $ p = 0.53 $, as before.

Conclusions

Based largely on the fact that the new study shows risks that are smaller than previous, smaller, studies, it seems to me that the evidence for the reality of the association is somewhat weaker than before.

Although the new study, unlike the earlier ones, shows signs for a relationship between the amount of read meat eaten and risk of death, the confounding factors (total calories eaten, weight, smoking etc) are so strong that the evidence for causality is critically dependent on the accuracy of the corrections for these factors, and even more dependent on their not being another factor that has not been included.

It can’t be said too often that if the association is not causal then refraining from eating red meat won’t have the slightest benefit. If it were, for example, the high calorie intake rather than eating meat that causes the risk, then stopping eating meat won’t help you in the slightest.

Even if the increased risk was entirely caused by eating meat, the worst consequence of eating red meat every day is to have a 53% chance of dying before someone who doesn’t eat much meat, rather than a 50% chance.

I won’t become a vegetarian just yet (or, at least if I do it will be on ethical grounds, not because of health risk).

Acknowledgment. I’m very grateful to Professor David Spiegelhalter for help and discussions about this post.