waiting
This is a post about Markovian queuing theory. But hang on, don’t run away. It isn’t so hard.
|
The idea came from my recent experience. On Friday 23 October, I was supposed to have a kidney removed at the Royal Marsden Hospital. At the very last minute the operation was cancelled. That is more irritating than serious. A delay of a few weeks poses no great risk for me. . |

|
The cancellation arose because there was no bed available in the High Dependency Unit (HDU), which is where nephrectomy patients go for a while after the operation. Was this a failure of the NHS? I think not and here’s why
The first reaction of a neighbour to this news was to say "that’s why I have private insurance". Well, wrong actually. For a start, at the Marsden private patients and NHS patients get identical treatment (the only difference on the NHS is that "you don’t get hot and cold running margaritas at your bedside", my surgeon said). And secondly, the provision of emergency beds poses a really difficult problem, which I’ll attempt to explain.
Bed provision raises a fascinating statistical question. How many beds must be available to make sure nobody is ever turned away? The answer, in principle, is an infinite number. In practice it is more than anyone can afford.
The HDU has eleven beds but let’s think about a simpler case to start with. If patients arrived regularly at a fixed rate, and each patient stayed for a fixed length of time. there would be no problem. Say, for example, that a patient arrived regularly at 10 am and 4 pm each day, and suppose that each patient stayed for exactly 46 hours. It’s pretty obvious that you’d need four beds. Each bed could take a patient every two days and there are two patients per day coming in. Allowing two hours for changing beds, all four beds would be occupied for essentially 100 percent of the time, actually 95% = 46 hours/48 hours).
Random arrivals
The problem arises because patients don’t arrive regularly and they don’t stay for a fixed length of time. What happens if patients arrive at random and stay for a random length of time? (We’ll get back to the meaning of ‘random’ in this context later.)
Suppose again that two patients per day arrive on average, and that each patient stays in the HDU for 46 hours on average. So the mean arrival rate, and the mean length of stay in the HDU are the same as in the first example. When there was no randomness, four beds coped perfectly.
But with random arrivals and random length of stay the situation is very different. With four beds, if a queue were allowed to build up, the average number of patients in the queue would be 21 and the average length of time a patient would spend waiting to get a bed would be 10.5 days. This would be an efficient use of resources because every time a bed was vacated it would be filled straight away from the queue. The resources would be used to the maximum possible extent:, 95%. But it would be terrible for patients. The length of the queue would, of course, fluctuate, as shown by this distribution (see below) of the queue length. Occasionally it might reach 100 or more.
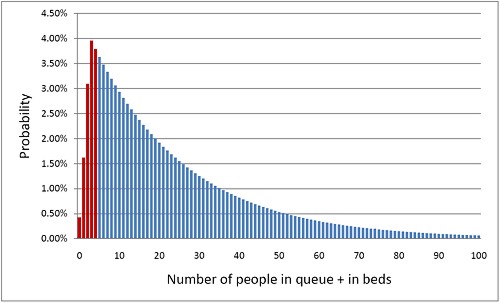
The histogram shows the total number of people in the system.The first five bins (red) represent the probabilities of 0, 1, 2, 3 or 4 beds being occupied. All the rest are in the queue.
What if you can’t queue?
For a High Dependency Unit or an Intensive Care Unit you can’t have a queue. If there is no bed, you are turned away. In the example just described, 91% of patients would have to wait, and that’s impossible in an HDU or ICU. The necessary statistical theory has been done for this case too (it is described as having zero queue capacity). Let’s look at the same case, with 4 beds, mean time between arrival of patients, 0.5 days, mean length of stay 1.917 days (46 hours).
|
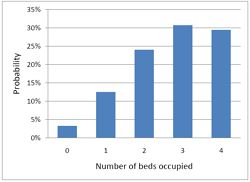
In this case there is no queue so the only possibilities are that 0, 1, 2, 3 or all 4 beds are occupied. The relative probabilities of these cases are shown on the right (they add up to 100% because there are no other possibilities). |
|
Despite the pressure on the unit, the randomness ensures that beds are by no means always occupied. All four are occupied for only 29% of the time and the average occupancy is 2.7 so the resources are used only 68% of the time (rather than 95% when a queue was allowed to form). Worse still, there is a 29% chance of the system being full, so you would be turned away.
So how many beds do you need? Clearly the more beds you have, the smaller the chance of anyone being turned away. But more beds means more cost and less efficiency. This is how it works out in our case.
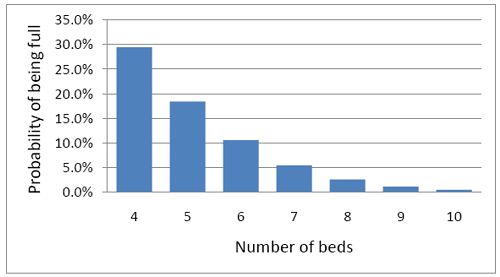
To get the chance of being turned away below 5%, rather than 29%, you’d have to double the number of beds from 4 to 8. But in doing so the beds would not be in use 68% of the time as with 4 beds, but for only 47% of the time.
|
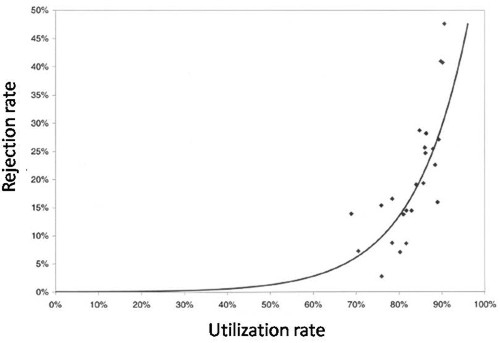
Looked at another way, if you try to increase the utilisation of beds, above 50 or 60%, then the rate at which patients get turned away goes shooting up exponentially. |
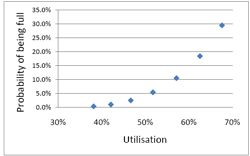
|
This isn’t inefficiency. It is an inevitable consequence of randomness in arrival times and lengths of stay.
A real life example
McManus et al. (2004) looked at all admissions to the medical–surgical Intensive Care Unit (ICU) of a large, urban children’s hospital in the USA during a 2-year period. (Anesthesiology 2004; 100:1271–6. Download pdf). Their Figure 2 shows the monthly average rejection rates mostly vary between 10 and 20%, so there is nothing unusual in there being no bed available in the private US medical system. For a period the rate of rejection reaches disastrous values, up to 47%. This happens, unsurprisingly, at times when the utilisation of beds was high.
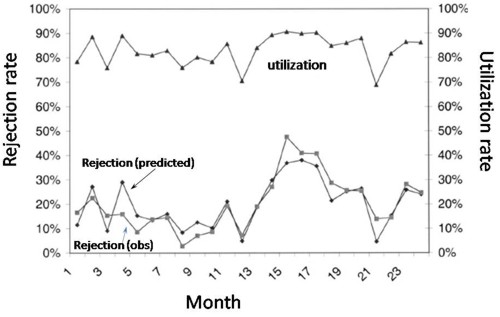
The observed relationship (McManus, Fig. 3) is very much as predicted above.with a very steep (roughly exponential) rise in rejection rate when the beds are in use for more than half the time.
How to do the calculations
You can get the message without reading this section. It’s included for those who want to know a bit more about what we mean when we say that patients arrive at random rather than at fixed intervals, and that durations of stay in the unit have random rather than fixed durations.
Consider the durations of stay in the unit. They are variable in length and the usual way to represent variability is to plot a distribution of the variable quantity. The best known sort of probability distribution is the bell-shaped curve known as the Gaussian distribution. This is shown at the top of the Figure (note that pdf stands for probability density function, not portable document format).
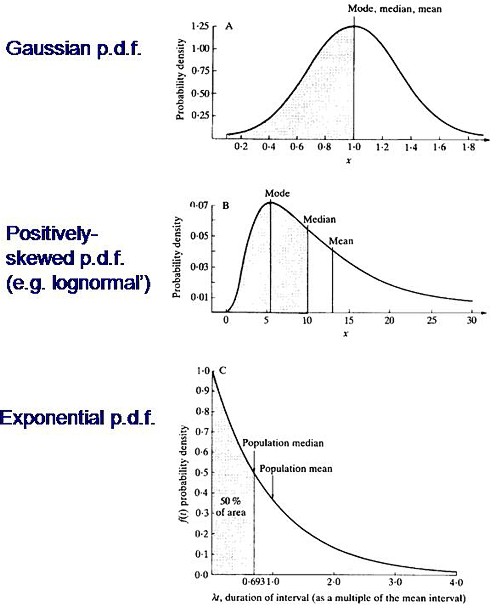
Not every sort of variability is described by a symmetrical bell-shaped curve. Quite often distributions with a positive skew are seen, like the middle example in the Figure. The distribution of incomes in the population have this sort of shape. Notice that more people earn less than average than earn more than average (the median is less than the mean). This can happen because those that earn less than average can’t get much less than average (unless we allow negative incomes), whereas bankers can earn (or at least be paid) a great deal more than average. The most frequent income (the peak of the distribution) is still smaller than the median.
An extreme form of a positively-skewed distribution is shown at the bottom. It is called the exponential distribution (because it has the shape of a decaying exponential curve). If this described personal incomes (and we are heading that way) it would mean that the most frequent income was zero and 63.2% of people earn less than average.
It is this last, rather unusual, sort of distribution that, in the simplest case, describes the lengths of random time intervals. This is getting very close to my day job. If an ion channel has a single open state, the lengths of individual ion channel openings is described by an exponential distribution.
|
The observation of an exponential distribution of durations is what would be predicted for a memoryless process, or Markov process. In the case of an ion channel, memoryless means that the probability of the channel shutting in the next microsecond is the same however long the channel has been open, This is exactly analogous to the fact that the probability of throwing a six with a die is exactly the same at each throw, regardless of how many sixes have been thrown before. |

Andrei A. Markov, 1856-1922 |
It is the simplest definition of a random length of time. For those who have done a bit of statistics, it is worth mentioning that if the number of events per unit time is described by a Poisson distribution, then the interval between events are exponentially-distributed. They are different ways of saying the same thing.
|
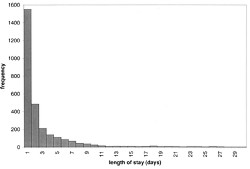
The lengths of stays in ICU in the McManus paper were roughly exponentially-distributed (right). The monthly average duration of stay ranged from 2.4 to 5.5 days, and average monthly admission rates to the 18 bed unit ranged from 4.6 to 6.2 patients per day. |
|
The monthly average percentage of patients who were turned away because there were no vacant beds varied widely, ranging from 3% up to a disastrous 47%
A technical note and an analogy with synapses
It’s intriguing to note that, in the simplest case, the time you’d spend waiting in a queue would have a simple exponential distribution (plus a discrete bit for the times when you don’t have to wait at all). The time you have to wait is the sum of all the lengths of stay of the people in front of you, and each of these lengths, in the case we discussing, is exponentially-distributed. If the queue was constant in length you can use a mathematical method known as convolution to show that the distribution of waiting time would follow a gamma distribution, a sort of distribution that goes through a peak, and eventually becomes Gaussian for long queues), However the queue is not fixed in length but its length is random (geometrically-distributed). It turns out that the distribution of the sum of a random number of exponentially distributed times is itself exponential. It is precisely this beautiful theorem that shows why the length of a burst of ion channel openings (which consists of the sum of a random number of exponentially-distributed open times, if you neglect the time spent in short shuttings) is, to a good approximation itself exponential, And that explains why the decay of synaptic currents is often close to following a simple exponential time course.
The calculations
The calculations for these graphs were done with a set of Excel add-in functions, Queueing Toolpak 4.0, which can be downloaded here. If this had been a paper of my own, rather than a blog post written in one weekend, I’d have done the algebra myself, just to be sure, The theory has much in common with that of single ion channels. Transitions between different states of the system can be described by transition rates or probabilities that don’t vary with time. The table, or matrix, of transition probabilities can be used to calculate the results, And if you want to know about the algebra of matrices, you could always apply for our summer workshop. There are some pictures from the workshop here.
Follow-up
Of course it is quite impossible for anyone who was around in the 60s to hear the name of a Russian mathematician without thinking of Tom Lehrer’s totally unjustified slur on another great Russian mathematician, Nicolai Ivanovich Lobachevsky. If you’ve never heard ‘Plagiarize’, you can hear it on Youtube. Sheer genius.
Why the size of the unit matters
This section was added as a result of a comment, below, from a statistician
At first glance one might think that if we quadruple the number of beds to 16 beds rather than 4, and we also quadruple the arrival rate to 8 rather than 2 per day, then the arrival rate per bed is the same and one might expect everything would stay the same.
As you say, it doesn’t.
If queueing was allowed, the mean queue length would be only slightly shorter, 18,7 rather than 20.9, but the mean time spent in the queue would fall from 10.5 days to 2.3 days.
In the more realistic case, with no queuing allowed, the rejection rate would fall from 29.4% to 15.5% and bed utilisation would increase from 68% to 81%. The rejection rate seems to fall roughly as the square root of the number of beds.
Clearly there is an advantage to having a big hospital with a big HDU.
Stochastic processes quite often behave unintuitive ways (unless you’ve spent years developing the right intuition).
