false discovery rate
This piece is almost identical with today’s Spectator Health article.
This week there has been enormously wide coverage in the press for one of the worst papers on acupuncture that I’ve come across. As so often, the paper showed the opposite of what its title and press release, claimed. For another stunning example of this sleight of hand, try Acupuncturists show that acupuncture doesn’t work, but conclude the opposite: journal fails, published in the British Journal of General Practice).
Presumably the wide coverage was a result of the hyped-up press release issued by the journal, BMJ Acupuncture in Medicine. That is not the British Medical Journal of course, but it is, bafflingly, published by the BMJ Press group, and if you subscribe to press releases from the real BMJ. you also get them from Acupuncture in Medicine. The BMJ group should not be mixing up press releases about real medicine with press releases about quackery. There seems to be something about quackery that’s clickbait for the mainstream media.
As so often, the press release was shockingly misleading: It said
Acupuncture may alleviate babies’ excessive crying Needling twice weekly for 2 weeks reduced crying time significantly
This is totally untrue. Here’s why.
|
Luckily the Science Media Centre was on the case quickly: read their assessment. The paper made the most elementary of all statistical mistakes. It failed to make allowance for the jelly bean problem. The paper lists 24 different tests of statistical significance and focusses attention on three that happen to give a P value (just) less than 0.05, and so were declared to be "statistically significant". If you do enough tests, some are bound to come out “statistically significant” by chance. They are false postives, and the conclusions are as meaningless as “green jelly beans cause acne” in the cartoon. This is called P-hacking and it’s a well known cause of problems. It was evidently beyond the wit of the referees to notice this naive mistake. It’s very doubtful whether there is anything happening but random variability. And that’s before you even get to the problem of the weakness of the evidence provided by P values close to 0.05. There’s at least a 30% chance of such values being false positives, even if it were not for the jelly bean problem, and a lot more than 30% if the hypothesis being tested is implausible. I leave it to the reader to assess the plausibility of the hypothesis that a good way to stop a baby crying is to stick needles into the poor baby. If you want to know more about P values try Youtube or here, or here. |
One of the people asked for an opinion on the paper was George Lewith, the well-known apologist for all things quackish. He described the work as being a "good sized fastidious well conducted study ….. The outcome is clear". Thus showing an ignorance of statistics that would shame an undergraduate.
On the Today Programme, I was interviewed by the formidable John Humphrys, along with the mandatory member of the flat-earth society whom the BBC seems to feel obliged to invite along for "balance". In this case it was professional acupuncturist, Mike Cummings, who is an associate editor of the journal in which the paper appeared. Perhaps he’d read the Science media centre’s assessment before he came on, because he said, quite rightly, that
"in technical terms the study is negative" "the primary outcome did not turn out to be statistically significant"
to which Humphrys retorted, reasonably enough, “So it doesn’t work”. Cummings’ response to this was a lot of bluster about how unfair it was for NICE to expect a treatment to perform better than placebo. It was fascinating to hear Cummings admit that the press release by his own journal was simply wrong.
Listen to the interview here
Another obvious flaw of the study is that the nature of the control group. It is not stated very clearly but it seems that the baby was left alone with the acupuncturist for 10 minutes. A far better control would have been to have the baby cuddled by its mother, or by a nurse. That’s what was used by Olafsdottir et al (2001) in a study that showed cuddling worked just as well as another form of quackery, chiropractic, to stop babies crying.
Manufactured doubt is a potent weapon of the alternative medicine industry. It’s the same tactic as was used by the tobacco industry. You scrape together a few lousy papers like this one and use them to pretend that there’s a controversy. For years the tobacco industry used this tactic to try to persuade people that cigarettes didn’t give you cancer, and that nicotine wasn’t addictive. The main stream media obligingly invite the representatives of the industry who convey to the reader/listener that there is a controversy, when there isn’t.
Acupuncture is no longer controversial. It just doesn’t work -see Acupuncture is a theatrical placebo: the end of a myth. Try to imagine a pill that had been subjected to well over 3000 trials without anyone producing convincing evidence for a clinically useful effect. It would have been abandoned years ago. But by manufacturing doubt, the acupuncture industry has managed to keep its product in the news. Every paper on the subject ends with the words "more research is needed". No it isn’t.
Acupuncture is pre-scientific idea that was moribund everywhere, even in China, until it was revived by Mao Zedong as part of the appalling Great Proletarian Revolution. Now it is big business in China, and 100 percent of the clinical trials that come from China are positive.
if you believe them, you’ll truly believe anything.
Follow-up
29 January 2017
Soon after the Today programme in which we both appeared, the acupuncturist, Mike Cummings, posted his reaction to the programme. I thought it worth posting the original version in full. Its petulance and abusiveness are quite remarkable.
I thank Cummings for giving publicity to the video of our appearance, and for referring to my Wikipedia page. I leave it to the reader to judge my competence, and his, in the statistics of clinical trials. And it’s odd to be described as a "professional blogger" when the 400+ posts on dcscience.net don’t make a penny -in fact they cost me money. In contrast, he is the salaried medical director of the British Medical Acupuncture Society.
It’s very clear that he has no understanding of the error of the transposed conditional, nor even the mulltiple comparison problem (and neither, it seems, does he know the meaning of the word ‘protagonist’).
I ignored his piece, but several friends complained to the BMJ for allowing such abusive material on their blog site. As a result a few changes were made. The “baying mob” is still there, but the Wikipedia link has gone. I thought that readers might be interested to read the original unexpurgated version. It shows, better than I ever could, the weakness of the arguments of the alternative medicine community. To quote Upton Sinclair:
“It is difficult to get a man to understand something, when his salary depends upon his not understanding it.”
It also shows that the BBC still hasn’t learned the lessons in Steve Jones’ excellent “Review of impartiality and accuracy of the BBC’s coverage of science“. Every time I appear in such a programme, they feel obliged to invite a member of the flat earth society to propagate their make-believe.
Acupuncture for infantile colic – misdirection in the media or over-reaction from a sceptic blogger?26 Jan, 17 | by Dr Mike Cummings So there has been a big response to this paper press released by BMJ on behalf of the journal Acupuncture in Medicine. The response has been influenced by the usual characters – retired professors who are professional bloggers and vocal critics of anything in the realm of complementary medicine. They thrive on oiling up and flexing their EBM muscles for a baying mob of fellow sceptics (see my ‘stereotypical mental image’ here). Their target in this instant is a relatively small trial on acupuncture for infantile colic.[1] Deserving of being press released by virtue of being the largest to date in the field, but by no means because it gave a definitive answer to the question of the efficacy of acupuncture in the condition. We need to wait for an SR where the data from the 4 trials to date can be combined. So what about the research itself? I have already said that the trial was not definitive, but it was not a bad trial. It suffered from under-recruiting, which meant that it was underpowered in terms of the statistical analysis. But it was prospectively registered, had ethical approval and the protocol was published. Primary and secondary outcomes were clearly defined, and the only change from the published protocol was to combine the two acupuncture groups in an attempt to improve the statistical power because of under recruitment. The fact that this decision was made after the trial had begun means that the results would have to be considered speculative. For this reason the editors of Acupuncture in Medicine insisted on alteration of the language in which the conclusions were framed to reflect this level of uncertainty. DC has focussed on multiple statistical testing and p values. These are important considerations, and we could have insisted on more clarity in the paper. P values are a guide and the 0.05 level commonly adopted must be interpreted appropriately in the circumstances. In this paper there are no definitive conclusions, so the p values recorded are there to guide future hypothesis generation and trial design. There were over 50 p values reported in this paper, so by chance alone you must expect some to be below 0.05. If one is to claim statistical significance of an outcome at the 0.05 level, ie a 1:20 likelihood of the event happening by chance alone, you can only perform the test once. If you perform the test twice you must reduce the p value to 0.025 if you want to claim statistical significance of one or other of the tests. So now we must come to the predefined outcomes. They were clearly stated, and the results of these are the only ones relevant to the conclusions of the paper. The primary outcome was the relative reduction in total crying time (TC) at 2 weeks. There were two significance tests at this point for relative TC. For a statistically significant result, the p values would need to be less than or equal to 0.025 – neither was this low, hence my comment on the Radio 4 Today programme that this was technically a negative trial (more correctly ‘not a positive trial’ – it failed to disprove the null hypothesis ie that the samples were drawn from the same population and the acupuncture intervention did not change the population treated). Finally to the secondary outcome – this was the number of infants in each group who continued to fulfil the criteria for colic at the end of each intervention week. There were four tests of significance so we need to divide 0.05 by 4 to maintain the 1:20 chance of a random event ie only draw conclusions regarding statistical significance if any of the tests resulted in a p value at or below 0.0125. Two of the 4 tests were below this figure, so we say that the result is unlikely to have been chance alone in this case. With hindsight it might have been good to include this explanation in the paper itself, but as editors we must constantly balance how much we push authors to adjust their papers, and in this case the editor focussed on reducing the conclusions to being speculative rather than definitive. A significant result in a secondary outcome leads to a speculative conclusion that acupuncture ‘may’ be an effective treatment option… but further research will be needed etc… Now a final word on the 3000 plus acupuncture trials that DC loves to mention. His point is that there is no consistent evidence for acupuncture after over 3000 RCTs, so it clearly doesn’t work. He first quoted this figure in an editorial after discussing the largest, most statistically reliable meta-analysis to date – the Vickers et al IPDM.[2] DC admits that there is a small effect of acupuncture over sham, but follows the standard EBM mantra that it is too small to be clinically meaningful without ever considering the possibility that sham (gentle acupuncture plus context of acupuncture) can have clinically relevant effects when compared with conventional treatments. Perhaps now the best example of this is a network meta-analysis (NMA) using individual patient data (IPD), which clearly demonstrates benefits of sham acupuncture over usual care (a variety of best standard or usual care) in terms of health-related quality of life (HRQoL).[3] |
30 January 2017
I got an email from the BMJ asking me to take part in a BMJ Head-to-Head debate about acupuncture. I did one of these before, in 2007, but it generated more heat than light (the only good thing to come out of it was the joke about leprechauns). So here is my polite refusal.
|
Hello Thanks for the invitation, Perhaps you should read the piece that I wrote after the Today programme Why don’t you do these Head to Heads about genuine controversies? To do them about homeopathy or acupuncture is to fall for the “manufactured doubt” stratagem that was used so effectively by the tobacco industry to promote smoking. It’s the favourite tool of snake oil salesman too, and th BMJ should see that and not fall for their tricks. Such pieces night be good clickbait, but they are bad medicine and bad ethics. All the best David |
In the course of thinking about metrics, I keep coming across cases of over-promoted research. An early case was “Why honey isn’t a wonder cough cure: more academic spin“. More recently, I noticed these examples.
“Effect of Vitamin E and Memantine on Functional Decline in Alzheimer Disease".(Spoiler -very little), published in the Journal of the American Medical Association. ”
and ” Primary Prevention of Cardiovascular Disease with a Mediterranean Diet” , in the New England Journal of Medicine (which had second highest altmetric score in 2013)
and "Sleep Drives Metabolite Clearance from the Adult Brain", published in Science
In all these cases, misleading press releases were issued by the journals themselves and by the universities. These were copied out by hard-pressed journalists and made headlines that were certainly not merited by the work. In the last three cases, hyped up tweets came from the journals. The responsibility for this hype must eventually rest with the authors. The last two papers came second and fourth in the list of highest altmetric scores for 2013
Here are to two more very recent examples. It seems that every time I check a highly tweeted paper, it turns out that it is very second rate. Both papers involve fMRI imaging, and since the infamous dead salmon paper, I’ve been a bit sceptical about them. But that is irrelevant to what follows.
Boost your memory with electricity
That was a popular headline at the end of August. It referred to a paper in Science magazine:
“Targeted enhancement of cortical-hippocampal brain networks and associative memory” (Wang, JX et al, Science, 29 August, 2014)
This study was promoted by the Northwestern University "Electric current to brain boosts memory". And Science tweeted along the same lines.

|
Science‘s link did not lead to the paper, but rather to a puff piece, "Rebooting memory with magnets". Again all the emphasis was on memory, with the usual entirely speculative stuff about helping Alzheimer’s disease. But the paper itself was behind Science‘s paywall. You couldn’t read it unless your employer subscribed to Science.
|
 |
|
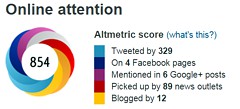
All the publicity led to much retweeting and a big altmetrics score. Given that the paper was not open access, it’s likely that most of the retweeters had not actually read the paper. |
|
When you read the paper, you found that is mostly not about memory at all. It was mostly about fMRI. In fact the only reference to memory was in a subsection of Figure 4. This is the evidence.
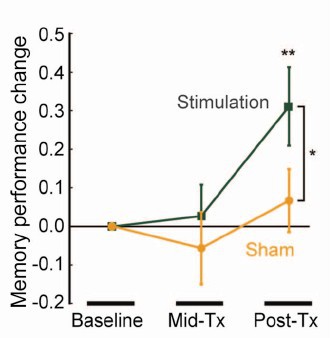
That looks desperately unconvincing to me. The test of significance gives P = 0.043. In an underpowered study like this, the chance of this being a false discovery is probably at least 50%. A result like this means, at most, "worth another look". It does not begin to justify all the hype that surrounded the paper. The journal, the university’s PR department, and ultimately the authors, must bear the responsibility for the unjustified claims.
Science does not allow online comments following the paper, but there are now plenty of sites that do. NHS Choices did a fairly good job of putting the paper into perspective, though they failed to notice the statistical weakness. A commenter on PubPeer noted that Science had recently announced that it would tighten statistical standards. In this case, they failed. The age of post-publication peer review is already reaching maturity
Boost your memory with cocoa
Another glamour journal, Nature Neuroscience, hit the headlines on October 26, 2014, in a paper that was publicised in a Nature podcast and a rather uninformative press release.
"Enhancing dentate gyrus function with dietary flavanols improves cognition in older adults. Brickman et al., Nat Neurosci. 2014. doi: 10.1038/nn.3850.".
The journal helpfully lists no fewer that 89 news items related to this study. Mostly they were something like “Drinking cocoa could improve your memory” (Kat Lay, in The Times). Only a handful of the 89 reports spotted the many problems.
A puff piece from Columbia University’s PR department quoted the senior author, Dr Small, making the dramatic claim that
“If a participant had the memory of a typical 60-year-old at the beginning of the study, after three months that person on average had the memory of a typical 30- or 40-year-old.”
|
Like anything to do with diet, the paper immediately got circulated on Twitter. No doubt most of the people who retweeted the message had not read the (paywalled) paper. The links almost all led to inaccurate press accounts, not to the paper itself. |
|
But some people actually read the paywalled paper and post-publication review soon kicked in. Pubmed Commons is a good site for that, because Pubmed is where a lot of people go for references. Hilda Bastian kicked off the comments there (her comment was picked out by Retraction Watch). Her conclusion was this.
"It’s good to see claims about dietary supplements tested. However, the results here rely on a chain of yet-to-be-validated assumptions that are still weakly supported at each point. In my opinion, the immodest title of this paper is not supported by its contents."
(Hilda Bastian runs the Statistically Funny blog -“The comedic possibilities of clinical epidemiology are known to be limitless”, and also a Scientific American blog about risk, Absolutely Maybe.)
NHS Choices spotted most of the problems too, in "A mug of cocoa is not a cure for memory problems". And so did Ian Musgrave of the University of Adelaide who wrote "Most Disappointing Headline Ever (No, Chocolate Will Not Improve Your Memory)",
Here are some of the many problems.
- The paper was not about cocoa. Drinks containing 900 mg cocoa flavanols (as much as in about 25 chocolate bars) and 138 mg of (−)-epicatechin were compared with much lower amounts of these compounds
- The abstract, all that most people could read, said that subjects were given "high or low cocoa–containing diet for 3 months". Bit it wasn’t a test of cocoa: it was a test of a dietary "supplement".
- The sample was small (37ppeople altogether, split between four groups), and therefore under-powered for detection of the small effect that was expected (and observed)
- The authors declared the result to be "significant" but you had to hunt through the paper to discover that this meant P = 0.04 (hint -it’s 6 lines above Table 1). That means that there is around a 50% chance that it’s a false discovery.
- The test was short -only three months
- The test didn’t measure memory anyway. It measured reaction speed, They did test memory retention too, and there was no detectable improvement. This was not mentioned in the abstract, Neither was the fact that exercise had no detectable effect.
- The study was funded by the Mars bar company. They, like many others, are clearly looking for a niche in the huge "supplement" market,
The claims by the senior author, in a Columbia promotional video that the drink produced "an improvement in memory" and "an improvement in memory performance by two or three decades" seem to have a very thin basis indeed. As has the statement that "we don’t need a pharmaceutical agent" to ameliorate a natural process (aging). High doses of supplements are pharmaceutical agents.
To be fair, the senior author did say, in the Columbia press release, that "the findings need to be replicated in a larger study—which he and his team plan to do". But there is no hint of this in the paper itself, or in the title of the press release "Dietary Flavanols Reverse Age-Related Memory Decline". The time for all the publicity is surely after a well-powered study, not before it.
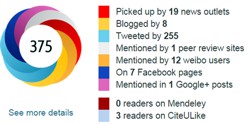
The high altmetrics score for this paper is yet another blow to the reputation of altmetrics.
One may well ask why Nature Neuroscience and the Columbia press office allowed such extravagant claims to be made on such a flimsy basis.
What’s going wrong?
These two papers have much in common. Elaborate imaging studies are accompanied by poor functional tests. All the hype focusses on the latter. These led me to the speculation ( In Pubmed Commons) that what actually happens is as follows.
- Authors do big imaging (fMRI) study.
- Glamour journal says coloured blobs are no longer enough and refuses to publish without functional information.
- Authors tag on a small human study.
- Paper gets published.
- Hyped up press releases issued that refer mostly to the add on.
- Journal and authors are happy.
- But science is not advanced.
It’s no wonder that Dorothy Bishop wrote "High-impact journals: where newsworthiness trumps methodology".
It’s time we forgot glamour journals. Publish open access on the web with open comments. Post-publication peer review is working
But boycott commercial publishers who charge large amounts for open access. It shouldn’t cost more than about £200, and more and more are essentially free (my latest will appear shortly in Royal Society Open Science).
Follow-up
Hilda Bastian has an excellent post about the dangers of reading only the abstract "Science in the Abstract: Don’t Judge a Study by its Cover"
4 November 2014
I was upbraided on Twitter by Euan Adie, founder of Almetric.com, because I didn’t click through the altmetric symbol to look at the citations "shouldn’t have to tell you to look at the underlying data David" and "you could have saved a lot of Google time". But when I did do that, all I found was a list of media reports and blogs -pretty much the same as Nature Neuroscience provides itself.
More interesting, I found that my blog wasn’t listed and neither was PubMed Commons. When I asked why, I was told "needs to regularly cite primary research. PubMed, PMC or repository links”. But this paper is behind a paywall. So I provide (possibly illegally) a copy of it, so anyone can verify my comments. The result is that altmetric’s dumb algorithms ignore it. In order to get counted you have to provide links that lead nowhere.
So here’s a link to the abstract (only) in Pubmed for the Science paper http://www.ncbi.nlm.nih.gov/pubmed/25170153 and here’s the link for the Nature Neuroscience paper http://www.ncbi.nlm.nih.gov/pubmed/25344629
It seems that altmetrics doesn’t even do the job that it claims to do very efficiently.
It worked. By later in the day, this blog was listed in both Nature‘s metrics section and by altmetrics. com. But comments on Pubmed Commons were still missing, That’s bad because it’s an excellent place for post-publications peer review.
This post is now a bit out of date: there is a summary of my more recent efforts (papers, videos and pop stuff) can be found on Prof Sivilotti’s OneMol pages.
What follows is a simplified version of part of a paper that appeared as a preprint on arXiv in July. It appeared as a peer-reviewed paper on 19th November 2014, in the new Royal Society Open Science journal. If you find anything wrong, or obscure, please email me. Be vicious.
There is also a simplified version, given as a talk on Youtube..
It’s a follow-up to my very first paper, which was written in 1959 – 60, while I was a fourth year undergraduate(the history is at a recent blog). I hope this one is better.
‘”. . . before anything was known of Lydgate’s skill, the judgements on it had naturally been divided, depending on a sense of likelihood, situated perhaps in the pit of the stomach, or in the pineal gland, and differing in its verdicts, but not less valuable as a guide in the total deficit of evidence” ‘George Eliot (Middlemarch, Chap. 45)
“The standard approach in teaching, of stressing the formal definition of a p-value while warning against its misinterpretation, has simply been an abysmal failure” Sellke et al. (2001) `The American Statistician’ (55), 62–71
The last post was about screening. It showed that most screening tests are useless, in the sense that a large proportion of people who test positive do not have the condition. This proportion can be called the false discovery rate. You think you’ve discovered the condition, but you were wrong.
Very similar ideas can be applied to tests of significance. If you read almost any scientific paper you’ll find statements like “this result was statistically significant (P = 0.047)”. Tests of significance were designed to prevent you from making a fool of yourself by claiming to have discovered something, when in fact all you are seeing is the effect of random chance. In this case we define the false discovery rate as the probability that, when a test comes out as ‘statistically significant’, there is actually no real effect.
You can also make a fool of yourself by failing to detect a real effect, but this is less harmful to your reputation.
It’s very common for people to claim that an effect is real, not just chance, whenever the test produces a P value of less than 0.05, and when asked, it’s common for people to think that this procedure gives them a chance of 1 in 20 of making a fool of themselves. Leaving aside that this seems rather too often to make a fool of yourself, this interpretation is simply wrong.
The purpose of this post is to justify the following proposition.
|
If you observe a P value close to 0.05, your false discovery rate will not be 5%. It will be at least 30% and it could easily be 80% for small studies.
|
This makes slightly less startling the assertion in John Ioannidis’ (2005) article, Why Most Published Research Findings Are False. That paper caused quite a stir. It’s a serious allegation. In fairness, the title was a bit misleading. Ioannidis wasn’t talking about all science. But it has become apparent that an alarming number of published works in some fields can’t be reproduced by others. The worst offenders seem to be clinical trials, experimental psychology and neuroscience, some parts of cancer research and some attempts to associate genes with disease (genome-wide association studies). Of course the self-correcting nature of science means that the false discoveries get revealed as such in the end, but it would obviously be a lot better if false results weren’t published in the first place.
How can tests of significance be so misleading?
Tests of statistical significance have been around for well over 100 years now. One of the most widely used is Student’s t test. It was published in 1908. ‘Student’ was the pseudonym for William Sealy Gosset, who worked at the Guinness brewery in Dublin. He visited Karl Pearson’s statistics department at UCL because he wanted statistical methods that were valid for testing small samples. The example that he used in his paper was based on data from Arthur Cushny, the first holder of the chair of pharmacology at UCL (subsequently named the A.J. Clark chair, after its second holder)
The outcome of a significance test is a probability, referred to as a P value. First, let’s be clear what the P value means. It will be simpler to do that in the context of a particular example. Suppose we wish to know whether treatment A is better (or worse) than treatment B (A might be a new drug, and B a placebo). We’d take a group of people and allocate each person to take either A or B and the choice would be random. Each person would have an equal chance of getting A or B. We’d observe the responses and then take the average (mean) response for those who had received A and the average for those who had received B. If the treatment (A) was no better than placebo (B), the difference between means should be zero on average. But the variability of the responses means that the observed difference will never be exactly zero. So how big does it have to be before you discount the possibility that random chance is all you were seeing. You do the test and get a P value. Given the ubiquity of P values in scientific papers, it’s surprisingly rare for people to be able to give an accurate definition. Here it is.
|
The P value is the probability that you would find a difference as big as that observed, or a still bigger value, if in fact A and B were identical.
|
If this probability is low enough, the conclusion would be that it’s unlikely that the observed difference (or a still bigger one) would have occurred if A and B were identical, so we conclude that they are not identical, i.e. that there is a genuine difference between treatment and placebo.
This is the classical way to avoid making a fool of yourself by claiming to have made a discovery when you haven’t. It was developed and popularised by the greatest statistician of the 20th century, Ronald Fisher, during the 1920s and 1930s. It does exactly what it says on the tin. It sounds entirely plausible.
What could possibly go wrong?
Another way to look at significance tests
One way to look at the problem is to notice that the classical approach considers only what would happen if there were no real effect or, as a statistician would put it, what would happen if the null hypothesis were true. But there isn’t much point in knowing that an event is unlikely when the null hypothesis is true unless you know how likely it is when there is a real effect.
We can look at the problem a bit more realistically by means of a tree diagram, very like that used to analyse screening tests, in the previous post.
In order to do this, we need to specify a couple more things.
First we need to specify the power of the significance test. This is the probability that we’ll detect a difference when there really is one. By ‘detect a difference’ we mean that the test comes out with P < 0.05 (or whatever level we set). So it’s analogous with the sensitivity of a screening test. In order to calculate sample sizes, it’s common to set the power to 0.8 (obviously 0.99 would be better, but that would often require impracticably large samples).
The second thing that we need to specify is a bit trickier, the proportion of tests that we do in which there is a real difference. This is analogous to the prevalence of the disease in the population being tested in the screening example. There is nothing mysterious about it. It’s an ordinary probability that can be thought of as a long-term frequency. But it is a probability that’s much harder to get a value for than the prevalence of a disease.
If we were testing a series of 30C homeopathic pills, all of the pills, regardless of what it says on the label, would be identical with the placebo controls so the prevalence of genuine effects, call it P(real), would be zero. So every positive test would be a false positive: the false discovery rate would be 100%. But in real science we want to predict the false discovery rate in less extreme cases.
Suppose, for example, that we test a large number of candidate drugs. Life being what it is, most of them will be inactive, but some will have a genuine effect. In this example we’d be lucky if 10% had a real effect, i.e. were really more effective than the inactive controls. So in this case we’d set the prevalence to P(real) = 0.1.
We can now construct a tree diagram exactly as we did for screening tests.
Suppose that we do 1000 tests. In 90% of them (900 tests) there is no real effect: the null hypothesis is true. If we use P = 0.05 as a criterion for significance then, according to the classical theory, 5% of them (45 tests) will give false positives, as shown in the lower limb of the tree diagram. If the power of the test was 0.8 then we’ll detect 80% of the real differences so there will be 80 correct positive tests.
The total number of positive tests is 45 + 80 = 125, and the proportion of these that are false positives is 45/125 = 36 percent. Our false discovery rate is far bigger than the 5% that many people still believe they are attaining.
In contrast, 98% of negative tests are right (though this is less surprising because 90% of experiments really have no effect).
The equation
You can skip this section without losing much.
As in the case of screening tests, this result can be calculated from an equation. The same equation works if we substitute power for sensitivity, P(real) for prevalence, and siglev for (1 – specificity) where siglev is the cut off value for “significance”, 0.05 in our examples.
The false discovery rate (the probability that, if a “signifcant” result is found, there is actually no real effect) is given by
\[FDR = \frac{siglev\left(1-P(real)\right)}{power.P(real) + siglev\left(1-P(real)\right) }\; \]
In the example above, power = 0.8, siglev = 0.05 and P(real) = 0.1, so the false discovery rate is
\[\frac{0.05 (1-0.1)}{0.8 \times 0.1 + 0.05 (1-0.1) }\; = 0.36 \]
So 36% of “significant” results are wrong, as found in the tree diagram.
Some subtleties
The argument just presented should be quite enough to convince you that significance testing, as commonly practised, will lead to disastrous numbers of false positives. But the basis of how to make inferences is still a matter that’s the subject of intense controversy among statisticians, so what is an experimenter to do?
It is difficult to give a consensus of informed opinion because, although there is much informed opinion, there is rather little consensus. A personal view follows. Colquhoun (1970), Lectures on Biostatistics, pp 94-95.
This is almost as true now as it was when I wrote it in the late 1960s, but there are some areas of broad agreement.
There are two subtleties that cause the approach outlined above to be a bit contentious. The first lies in the problem of deciding the prevalence, P(real). You may have noticed that if the frequency of real effects were 50% rather than 10%, the approach shown in the diagram would give a false discovery rate of only 6%, little different from the 5% that’s embedded in the consciousness of most experimentalists.
But this doesn’t get us off the hook, for two reasons. For a start, there is no reason at all to think that there will be a real effect there in half of the tests that we do. Of course if P(real) were even bigger than 0.5, the false discovery rate would fall to zero, because when P(real) = 1, all effects are real and therefore all positive tests are correct.
There is also a more subtle point. If we are trying to interpret the result of a single test that comes out with a P value of, say, P = 0.047, then we should not be looking at all significant results (those with P < 0.05), but only at those tests that come out with P = 0.047. This can be done quite easily by simulating a long series of t tests, and then restricting attention to those that come out with P values between, say, 0.045 and 0.05. When this is done we find that the false discovery rate is at least 26%. That’s for the best possible case where the sample size is good (power of the test is 0.8) and the prevalence of real effects is 0.5. When, as in the tree diagram, the prevalence of real effects is 0.1, the false discovery rate is 76%. That’s enough to justify Ioannidis’ statement that most published results are wrong.
One problem with all of the approaches mentioned above was the need to guess at the prevalence of real effects (that’s what a Bayesian would call the prior probability). James Berger and colleagues (Sellke et al., 2001) have proposed a way round this problem by looking at all possible prior distributions and so coming up with a minimum false discovery rate that holds universally. The conclusions are much the same as before. If you claim to have found an effects whenever you observe a P value just less than 0.05, you will come to the wrong conclusion in at least 29% of the tests that you do. If, on the other hand, you use P = 0.001, you’ll be wrong in only 1.8% of cases. Valen Johnson (2013) has reached similar conclusions by a related argument.
A three-sigma rule
As an alternative to insisting on P < 0.001 before claiming you’ve discovered something, you could use a 3-sigma rule. In other words, insist that an effect is at least three standard deviations away from the control value (as opposed to the two standard deviations that correspond to P = 0.05).
The three sigma rule means using P= 0.0027 as your cut off. This, according to Berger’s rule, implies a false discovery rate of (at least) 4.5%, not far from the value that many people mistakenly think is achieved by using P = 0.05 as a criterion.
Particle physicists go a lot further than this. They use a 5-sigma rule before announcing a new discovery. That corresponds to a P value of less than one in a million (0.57 x 10−6). According to Berger’s rule this corresponds to a false discovery rate of (at least) around 20 per million. Of course their experiments can’t be randomised usually, so it’s as well to be on the safe side.
Underpowered experiments
All of the problems discussed so far concern the near-ideal case. They assume that your sample size is big enough (power about 0.8 say) and that all of the assumptions made in the test are true, that there is no bias or cheating and that no negative results are suppressed. The real-life problems can only be worse. One way in which it is often worse is that sample sizes are too small, so the statistical power of the tests is low.
The problem of underpowered experiments has been known since 1962, but it has been ignored. Recently it has come back into prominence, thanks in large part to John Ioannidis and the crisis of reproducibility in some areas of science. Button et al. (2013) said
“We optimistically estimate the median statistical power of studies in the neuroscience field to be between about 8% and about 31%”
This is disastrously low. Running simulated t tests shows that with a power of 0.2, not only do you have only a 20% chance of detecting a real effect, but that when you do manage to get a “significant” result there is a 76% chance that it’s a false discovery.
And furthermore, when you do find a “significant” result, the size of the effect will be over-estimated by a factor of nearly 2. This “inflation effect” happens because only those experiments that happen, by chance, to have a larger-than-average effect size will be deemed to be “significant”.
What should you do to prevent making a fool of yourself?
The simulated t test results, and some other subtleties, will be described in a paper, and/or in a future post. But I hope that enough has been said here to convince you that there are real problems in the sort of statistical tests that are universal in the literature.
The blame for the crisis in reproducibility has several sources.
One of them is the self-imposed publish-or-perish culture, which values quantity over quality, and which has done enormous harm to science.
The mis-assessment of individuals by silly bibliometric methods has contributed to this harm. Of all the proposed methods, altmetrics is demonstrably the most idiotic. Yet some vice-chancellors have failed to understand that.
Another is scientists’ own vanity, which leads to the PR department issuing disgracefully hyped up press releases.
In some cases, the abstract of a paper states that a discovery has been made when the data say the opposite. This sort of spin is common in the quack world. Yet referees and editors get taken in by the ruse (e.g see this study of acupuncture).
The reluctance of many journals (and many authors) to publish negative results biases the whole literature in favour of positive results. This is so disastrous in clinical work that a pressure group has been started; altrials.net “All Trials Registered | All Results Reported”.
Yet another problem is that it has become very hard to get grants without putting your name on publications to which you have made little contribution. This leads to exploitation of young scientists by older ones (who fail to set a good example). Peter Lawrence has set out the problems.
And, most pertinent to this post, a widespread failure to understand properly what a significance test means must contribute to the problem. Young scientists are under such intense pressure to publish, they have no time to learn about statistics.
Here are some things that can be done.
- Notice that all statistical tests of significance assume that the treatments have been allocated at random. This means that application of significance tests to observational data, e.g. epidemiological surveys of diet and health, is not valid. You can’t expect to get the right answer. The easiest way to understand this assumption is to think about randomisation tests (which should have replaced t tests decades ago, but which are still rare). There is a simple introduction in Lectures on Biostatistics (chapters 8 and 9). There are other assumptions too, about the distribution of observations, independence of measurements), but randomisation is the most important.
- Never, ever, use the word “significant” in a paper. It is arbitrary, and, as we have seen, deeply misleading. Still less should you use “almost significant”, “tendency to significant” or any of the hundreds of similar circumlocutions listed by Matthew Hankins on his Still not Significant blog.
- If you do a significance test, just state the P value and give the effect size and confidence intervals (but be aware that this is just another way of expressing the P value approach: it tells you nothing whatsoever about the false discovery rate).
- Observation of a P value close to 0.05 means nothing more than ‘worth another look’. In practice, one’s attitude will depend on weighing the losses that ensue if you miss a real effect against the loss to your reputation if you claim falsely to have made a discovery.
- If you want to avoid making a fool of yourself most of the time, don’t regard anything bigger than P < 0.001 as a demonstration that you’ve discovered something. Or, slightly less stringently, use a three-sigma rule.
Despite the gigantic contributions that Ronald Fisher made to statistics, his work has been widely misinterpreted. We must, however reluctantly, concede that there is some truth in the comment made by an astute journalist:
“The plain fact is that 70 years ago Ronald Fisher gave scientists a mathematical machine for turning baloney into breakthroughs, and °flukes into funding. It is time to pull the plug“. Robert Matthews Sunday Telegraph, 13 September 1998.
There is now a video on YouTube that attempts to explain explain simply the essential ideas. The video has now been updated. The new version has better volume and it used term ‘false positive risk’, rather than the earlier term ‘false discovery rate’, to avoid confusion with the use of the latter term in the context of multiple comparisons.
The false positive risk: a proposal concerning what to do about p-values (version 2)
Follow-up
31 March 2014 I liked Stephen Senn’s first comment on twitter (the twitter stream is storified here). He said ” I may have to write a paper ‘You may believe you are NOT a Bayesian but you’re wrong'”. I maintain that the analysis here is merely an exercise in conditional probabilities. It bears a formal similarity to a Bayesian argument, but is free of more contentious parts of the Bayesian approach. This is amplified in a comment, below.
4 April 2014
I just noticed that my first boss, Heinz Otto Schild.in his 1942 paper about the statistical analysis of 2+2 dose biological assays (written while he was interned at the beginning of the war) chose to use 99% confidence limits, rather than the now universal 95% limits. The later are more flattering to your results, but Schild was more concerned with precision than self-promotion.